Trascendental curves   

The possibility of considering curves "generic"sheds a different light on many classic problems, especially those regarding squaring and tangents.

To square a figure literally means finding an equivalent square to the given figure. Obviously, the solution to a squaring problem depends on the tools considered acceptable for the construction of the required square. For example, when speaking about the classical problem of the squaring of the circle, a ruler and compass are considered appropriate. The problem thus formulated was only solved in the last century, with the demonstration of the impossibility of such a construction. If on the other hand, more tools are accepted, such as the "quadratrice of Ippia", a positive answer is found to the problem - one that has been well known since Greek times.

If limited to the use of ruler and compasses, few positive results can be obtained. Hippocrates managed to square lunes, the first example of exact squaring of a curvilinear figure. Archimedes discovered the squaring of parabolas. Similarly, classic surveyors solved, in some cases, the problem of tangents, or rather that of determining the straight line best approaching a given curve when close to one of its points. The Greeks determined the tangents to circles or conic sections and also to other particular curves.

In the new Cartesian formulation the two problems assume different aspects: rather than squaring this or that figure, or finding the tangent to this or that line, what must be found is a uniform method which allows one to trace the tangent to an arbitrary curve or to provide the procedure to square a figure delimited by any curve.

The first of these problems,which was partly solved by Descartes, was to lead to the discovery of differential calculus by Newton (1643-1727) and Leibniz (1646-1716). The second was to be the object of integral calculus.

More difficult is the so called inverse problem of the tangent, or in modern terms, the integration of a differential equation.

From the geometrical point of view, the problem consists in finding a curve, knowing a relationship between its points and the relative tangents. Analytically, it translates in an equation which binds the variables x and y to their differentials. These equations lead to the solutions not only of geometrical problems (such as the so called Baune's problem , the first to be formulated in terms of differential equations ) but also to a number of physics problems - especially mechanical ones - first of all, finding the trajectory of a body subject to a given force. Such are the falls of bodies and in general the motion of a body in the void or in a resistant medium and the defining of the orbits of planets, subject to an attractive force proportional to the inverse of the squared distance from the sun. Both problems are looked into by Newton in his Principia. A few years later Leonhard Euler (1707-1783) submitted all mechanics to calculus.

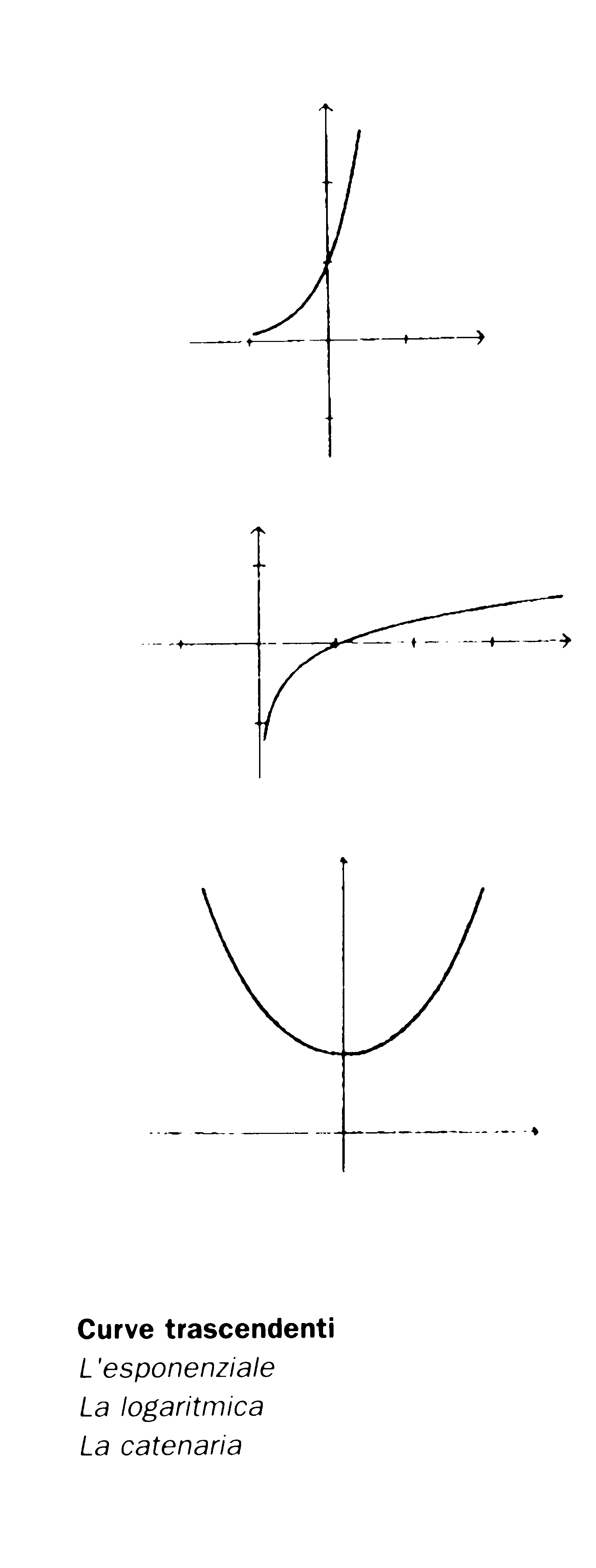
Differential equations bring to the fore a new class of curves, which only emerged sporadically in the course of the 17th century - transcendental curves. These are curves which cannot be expressed through algebraic expressions but which, in order to be described analytically, require the introduction of new functions, among which are trigonometric equations, logarithms and exponentials.

The first problem that can be traced back to a differential equation, the De Baune's problem, has the exponential curve of equation y = e^x as solution. The same curve, of equation x = log y,if seen inverting the two axes interferes in the problem of the squaring of the hyperbola. As new problems, impossible to solve before the invention of calculus, come to be faced, new transcendent curves are discovered. The first problem faced and successfully solved is that of a chain hanging from the ends: its solution is a curve, the catenary, of equation

y = (e^x+e^-x)/2.

A second success of new calculus was the definition of the brachistochrone, the curve which reduces to the minimum the falling time from one of its ends to the other.

More precisely, suppose we fix two points P and Q, the first higher than the second but not on the vertical line, and let a body fall from P to Q sliding on a curve which joins the two points. The problem now is: among all the curves joining P to Q, which is the one that reduces the falling time to the minimum? It isn't the straight line joining the two points as it might seem at first sight. In fact, in order to reduce falling time it is expedient to start almost vertically, so to gain speed straight away, even if risking a longer path.

In this case the solution is a cycloid, the curve described by one point of a circle which rotates without grazing.

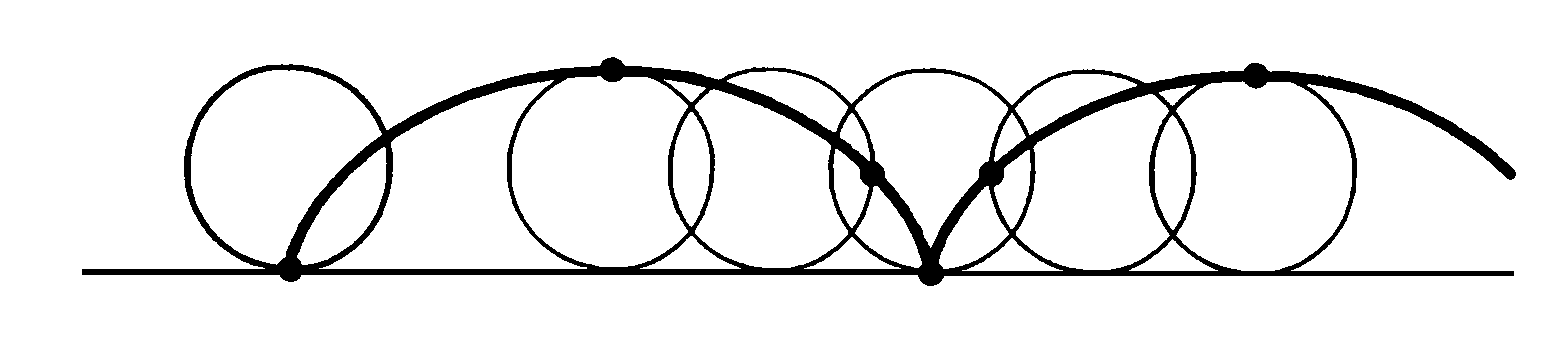
The same curve represents the solution to another problem too. Suppose you put a little ball onto a profile shaped like a semicircle and let it go. The ball will start swinging back and forth, while the time it'll take to complete one oscillation will decrease as the magnitude of the oscillation gets smaller, remaining almost constant for small oscillations. One should then ask: is there a curve on which any oscillation, big or small, takes the same time? The answer is affirmative: the isochrone curve is, again, the cycloid.