Curves and equations   

Both ruler and compasses, and conic sections belong to the scientific heritage of classic Greece and to some extent we embody this heritage. More than a few other lines can be found in the works by Greek mathematicians - spirals, quadratrices, conchoids, cissoids and in some cases even special curves like the helices of Pappo (III century DA.D.) on the surface of the sphere. But, in any case, these particular curves derive more from the imagination of this or that surveyor, than from an internal mathematical internal dynamic, which was, instead, slowly withering. The appearance of these particular curves was not a sign of scientific progress, but rather a symptom of a lack of inspiration and increasing levels of self-indulgence.

Apart, perhaps, from conic sections, all the curves of Greek geometry are "nominated" curves. All of them are defined through characteristic properties valid only for themselves. Each one needs specific methods that cannot be applied in other situations.

In order to leave this limited world, a radically different point of view was required - a method that could applied to all curves without being specific to any of them. A method by which the general gained at the expense of the minute details of procedure.

A decisive step consisted in the introduction of the cartesian coordinates, which are called after the philosopher and mathematician Réné Descartes (1596-1650). Any point P of the plane can be found through two numbers (x, y) that are the distances from two perpendicular lines. these last ones are the cartesian axis, and the numbers x and y the cartesian coordinates of the point P. The x is called abscissa, and y ordinate of the point P. The abscissa is positive on the right and negative on the left, the ordinate positive high up and negative low down.

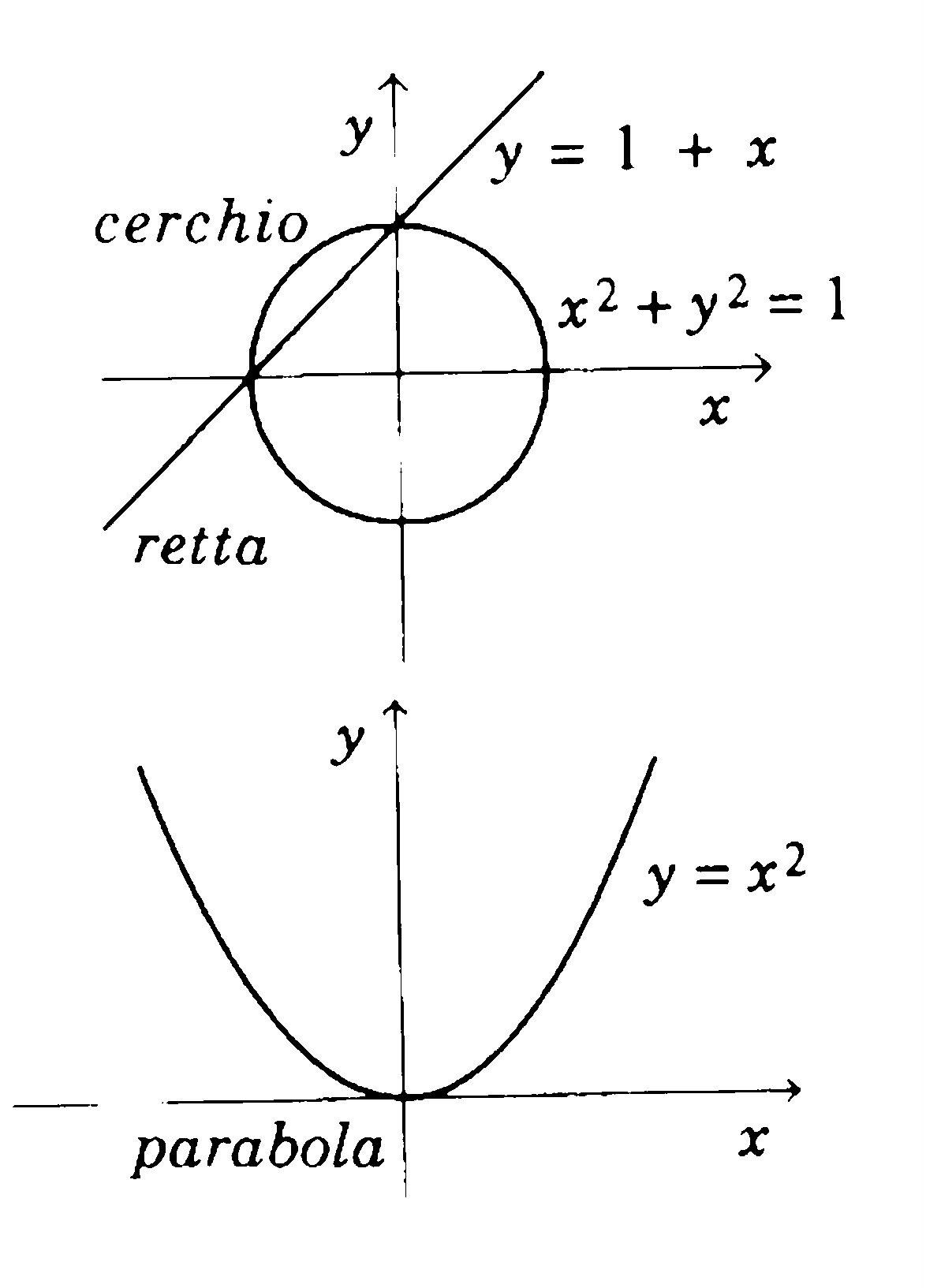
When its coordinates x and y vary in all possible ways, the point P describes the whole plane. If, instead, the coordinates of P are tied up by an equation, the corresponding point will not be able to move arbitrarily on the plane, but will be forced to follow a curve. For instance, the equation y=2 describes a straight horizontal line, x²+y²=1 is the equation of a circle and y=x² of a parabola.

Generally, an algebraic equation F(x,y)=0, where F(x,y) is a polinomy in variables x and y, can be connected to a curve that is the place of points whose coordinates satisfy the equation under consideration. The latter can be relatively simple, like the one expressing a line or a circle, but also quite complex, like for example x²⁷+y⁴-x³y¹³=1. The most complex curves can be described through equations. Bernoully claimed that he could write the equation of the face of a man!

A method to obtain the points of the curves consists in fixing the value of one of its coordinates, for example x=1, thus obtaining the equation F(1,y)=0, only in the y. By solving the latter, one or more values of y can be obtained, individuating one or more points of the curve, its correspondence to the abscissa x=1. Taking different values for x, various points of the curve are obtained and the curve can be drawn with the necessary precision.

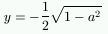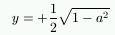For example, to draw the points of the ellipse x² + 4y² = 1, we make x = a, and we solve the equation a²+4y² = 1. The solutions of this equation are given by 4y² = 1-a² and, therefore, if -1<a< there are two solutions    e   , while if a = 1 meaning a = -1 there is only the solution y = 0, and if a>-1 there are no solutions. Attributing finally, to a, different values comprised between -1 and 1, and reporting the corresponding points on the diagram, we obtain a series of points of the curve.

It should be noted that this is not the best procedure to trace this or that particular curve. For example, a circle can be drawn better and more easily with a compass, rather than by constructing its points verifying the equation x²+y² = 1. The same applies to the ellipse, conic sections and practically to all particular curves. For each, it is possible to make an instrument to trace it accurately and faster than can be done employing the method of successive determination of its points. This has, however, an important decisive advantage - that of being a general method. It is true that for each curve a tool can be invented to trace it, but, changing the curve we will have to abandon the mechanism used to trace it and employ another one intended for the new one. However, the method of tracing points is independent from the curve in question, which only enters into its equation to differenciate the otherwise uniform procedure. It is precisely the possibility of study methods and general procedures that makes the new cartesian formulation more adaptable and powerful than the constructing techniques of classic geometry.

Curves can, therefore, be drawn by points, solving some equations, and, conversely, equations can be solved through the intersection of two curves.

If F(x,y) = 0 and G(x,y) = 0 are the equations of two curves, the points belonging to the intersection of these will have to verify both equations. Now, one of the two variables can be derived, for example y in function of x, from the first equation, and inserting the value y(x) found in the second, one obtains an equation P(x) = 0 only in x, the solutions of which are the abscissas of the points of intersection of the two curves. If, therefore, one wants to solve the equation P(x) = 0,two curves F(x,y) and G(x,y) must be found so that the given equation is the one resulting from the elimination of y. The abscissas of the points of intersection of the two curves give the solution to the equation.

Naturally, the same equation P(x) = 0 can be obtained through different choices of curves, or of the functions F(x,y) and G(x,y). Doing so for example, the solutions x₁ and x₂ of the second grade equation

x²+x=4 can be constructed intersecting the line y = x with the parabola x²+y = 4,or with the hyperbole xy+x = 4, or with the circle (x+1)²+y² = 9, that have the centre in the point (-1,0) and radius 3. In fact, replacing the value x into y in the equation of the circle, (x+1)²+x² = 9, or 2x²+2x+1 = 9 can be obtained and then x²+x = 4. Among all of them the one corresponding to the best criteria of simplicity can be chosen for example the last one which only has the intervention line and circle and can, therefore, be drawn with a ruler and compass.

If the grade of the equation is higer than 2, lines and circles are no longer sufficient, and it is necessary to resort to curves such as conic sections or even others less familiar. For example, the solutions of the equation x⁴+x²+3x = 1 can be obtained by intersecting the circle x²+y²+3x =1 with the parabola y = x². As the grade of the equation increases, more complex curves become necessary.