The curvature   

The developments of infinitesimal calculus in the seventeenth century allowed for remarkable progress in the study of the properties of curves. We have seen that, among all the straight lines passing through a point P of a curve, the tangent is the one that best approximates the curve in proximity to the point P. To arrive at a better approximation, one needs to go beyond straight lines, and employ in particular simple curves as, for example, circumferences. The process is similar to that one used for the tangent - among all the circles passing through P, there is one that best fits the course of the curve in proximity to P. This circle, with a centre that is placed on the perpendicular to the curve (or perpendicular to its tangent, which is the same), is known as an osculating circle.

We can then measure the curvature of a curve. The tangent allows us to determine the direction of curve C. If we imagine a point moving along C, we can presume that, at any time, the movement takes place in the direction of the tangent. Similarily, the curvature of C will be given as the one of the osculating circle. Since a circle becomes more curved as its radius becomes shorter, it is possible to measure the curvature of C through the inverse of the radius of the osculating circle, or rather the radius of the curvature.

Driving on a curve at speed v, one is subjected to a centrifugal force proportional to v²/r. It is then possible to see that to avoid driving off the road it's necessary to slow down where the radius of curvature gets shorter - where the curvature increases. In other words, one can drive faster on wider curves, but must slow down on tight ones. On a straight road there is no centrifugal force, as a straight line has zero curvature.

As the point P moves on the curve, the centres of curvature (centres of osculating circles) will describe a second curve, which is called the evolute of the former. This curve is also the envelope of the perpendicular lines to the given curve.

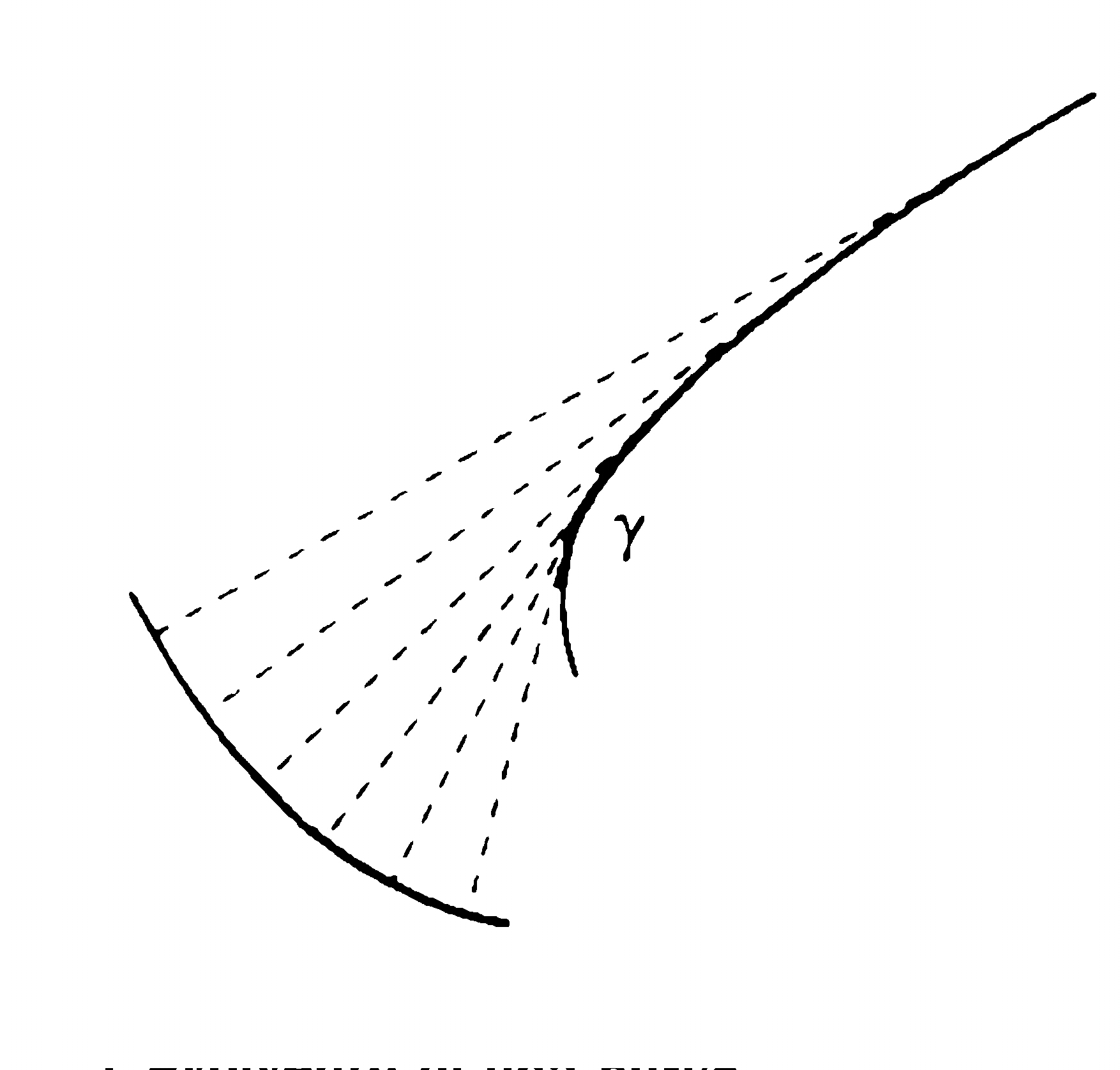Reciprocally, the first curve is called the involute of the second. The involute of a curve C can be obtained concretely by cutting a board along the profile of C and sticking a thread along this profile, then unwinding it bit by bit, keeping the loose part always taut. The free end of the thread will then describe the involute of C.

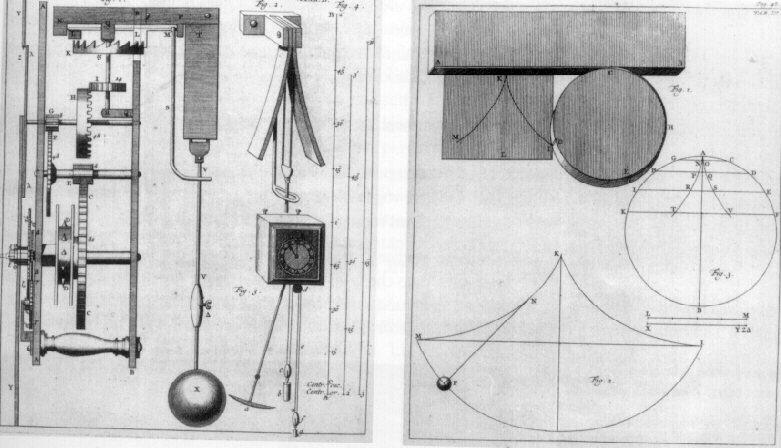
The relation evolute-involute can also be useful to solve technical problems. When we referred to oscillations, we said that we have a perfect isochronism when the motion takes place along a cycloid. Naturally, the isochronism is important in making pendulum clocks. But how is it possible to make a pendulum move along a cycloid? A profile with the shape of a cycloid can be made, and then the weight of the pendulum allowed to roll along it. But without considering the difficulty of assuring a regular movement, the friction of the weight along the profile would be enough to make the pendulum stop in a few minutes. If, instead, we attach the weight to a string that we will hang from the other end, the pendulum will describe a circle that is not isochronic.

The problem can be solved by making two guides that will be placed at the two sides of the suspension point. In this way, the string of the pendulum will not be able to move freely, but will have to partially follow the guide. The end of the pendulum will then describe the involute of the profile. Then, we need to trace the profile in such a way that its involute is a cycloid, or better, with the shape of the evolute of a cycloid. The latter is still a cycloid that is the only curve to be both evolute and involute of itself. Therefore, by making two guides with the shape of a cycloid, a perfectly isochronic pendulum will be obtained.