A Museum for Mathematics
| The Garden of Archimedes
A Museum for Mathematics |
The geometry of curves:
|
| |
| |
Even though they contain indications of ancient, practical origins, the Euclidean Elements are a late work where the axiomatic deductive structure is developed completely, even if not with absolute rigor. Their variety shows the legacy of generations of surveyors who, from the procedures learnt from the Egyptians, were able to create a totally new science as a theoretical system much richer than those who pulled ropes or traced circles could have imagined.
Nonetheless, some problems remained persistently beyond the scope of the line and circle, even when geometry was moved to the world of paper, ruler and compasses. Among them are three classic problems: the duplication of the cube, the trisection of the angle and the quadrature of the circle.
According to legend, when Greece was victim of a great epidemic,
a delegation went to the oracle of Delo to ask respite. The response
of the oracle was that the rage of the Gods would be placated only when the
altar dedicated to them, which had the shape of a cube, was be replaced by
one of the same shape but twice the size. The messengers, industrious but
not very wise, ordered an altar to be built, again in the shape of a cube,
with the side twice as long as that of the original.
The epidemic didn't stop and the oracle was consulted
again. On that occasion it was discovered that the new altar
was not twice as big as the former one but eight times bigger,
being, in fact, the volume of the cube with side a equal
3the one with side 2a will have volume
(2a)3
If, on the other hand, the cube with side a needs to be doubled, it is
necessary to build another one with side 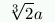 , so that its volume is
, so that its volume is 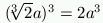 .
.
Leaving aside the legend and taking an exclusively geometrical
point of view,
the problem consists in, given a segment of length a, drawing
a second segment,
with length
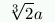 . Now, while it is easy
to build a segment
with length
. Now, while it is easy
to build a segment
with length 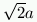 with ruler and
compasses (it is
sufficient to build a square of side a, the diagonal of which
is
with ruler and
compasses (it is
sufficient to build a square of side a, the diagonal of which
is 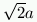 long),
and then double a square (the square built on the diagonal of
the former
one is suitable), to double the cube is not as
simple. Instead, it was
demonstrated, even in relatively recent times, that the
problem cannot
be solved using exclusively a ruler and compasses. The problem
of Delo
requires the employment of more complex tools and techniques.
long),
and then double a square (the square built on the diagonal of
the former
one is suitable), to double the cube is not as
simple. Instead, it was
demonstrated, even in relatively recent times, that the
problem cannot
be solved using exclusively a ruler and compasses. The problem
of Delo
requires the employment of more complex tools and techniques.
The same occurs with the other problems. For those, the surveyors invent new curves, pushing themselves beyond the limits of lines and circles. Ippia from Elide (V century B.C.) invented the quadratrix, a curve that he used to obtain the quadrature of the circle and the trisection of the angle.
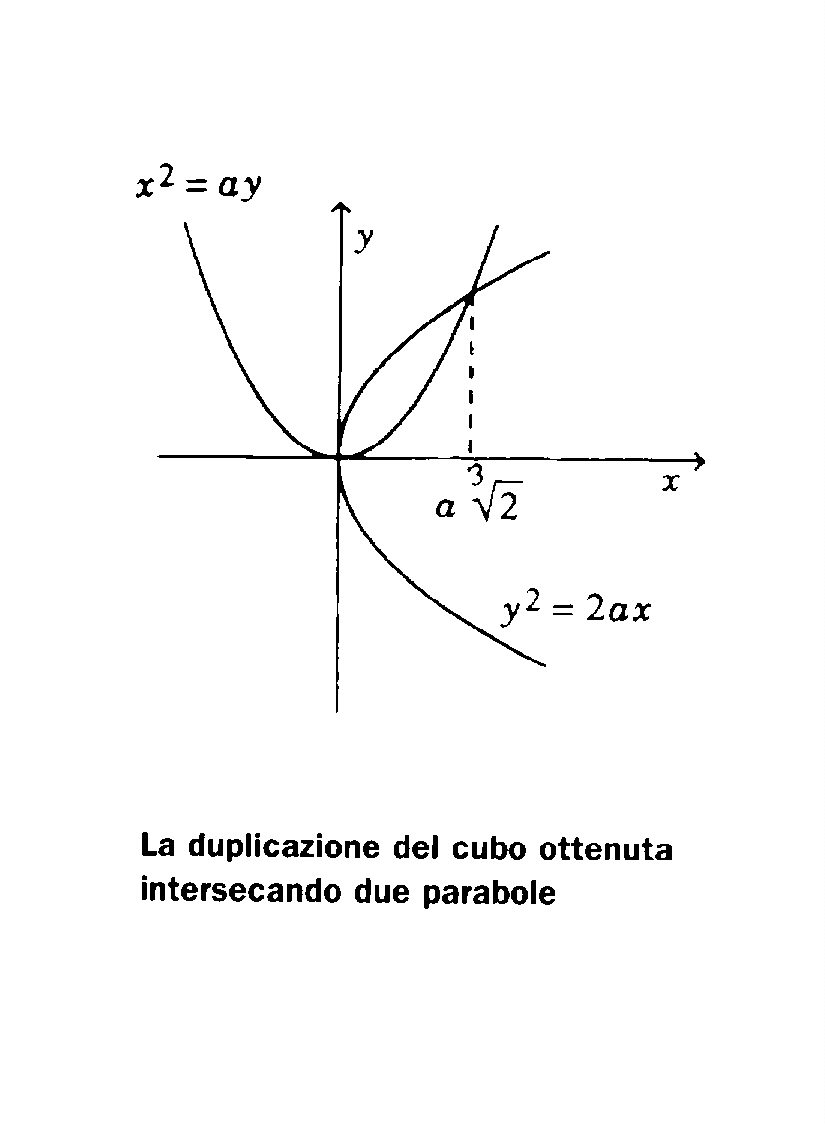 Later, the problem of the duplication of the cube was solved by
Archita from
Taranto (or maybe by Menecmo from Proconneso, who also lived around
the 400 B.C.)
through the intersection of two parabolas, and by Diocle (II century
B.C.)
through a new curve, the cissoid. The method of Archita is very
ingenious and
easy to describe, using the modern system of Cartesian
geometry. Considering
two parabolas with equation
y2
= 2ax e x2 = ay. If the point with coordinates
(x,y) belongs
to both curves, we'll have x4 =
a2y2 =2a3x, from which,
excluding the solution
x=0, is found x3=2a3, and therefore
Later, the problem of the duplication of the cube was solved by
Archita from
Taranto (or maybe by Menecmo from Proconneso, who also lived around
the 400 B.C.)
through the intersection of two parabolas, and by Diocle (II century
B.C.)
through a new curve, the cissoid. The method of Archita is very
ingenious and
easy to describe, using the modern system of Cartesian
geometry. Considering
two parabolas with equation
y2
= 2ax e x2 = ay. If the point with coordinates
(x,y) belongs
to both curves, we'll have x4 =
a2y2 =2a3x, from which,
excluding the solution
x=0, is found x3=2a3, and therefore
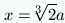 .
In conclusion, by intersecting the two parabolas, a point with
the side of the
double cube as abscissas can be obtained.
.
In conclusion, by intersecting the two parabolas, a point with
the side of the
double cube as abscissas can be obtained.
Naturally, we have simplified the description of the process of Archita, who, not knowing cartesian geometry and in particular the use of coordinates, employed purely geometric methods. What is most interesting is that certain curves appear in the demonstration for the first time. These were to be the object of study for many centuries to come: conic sections.