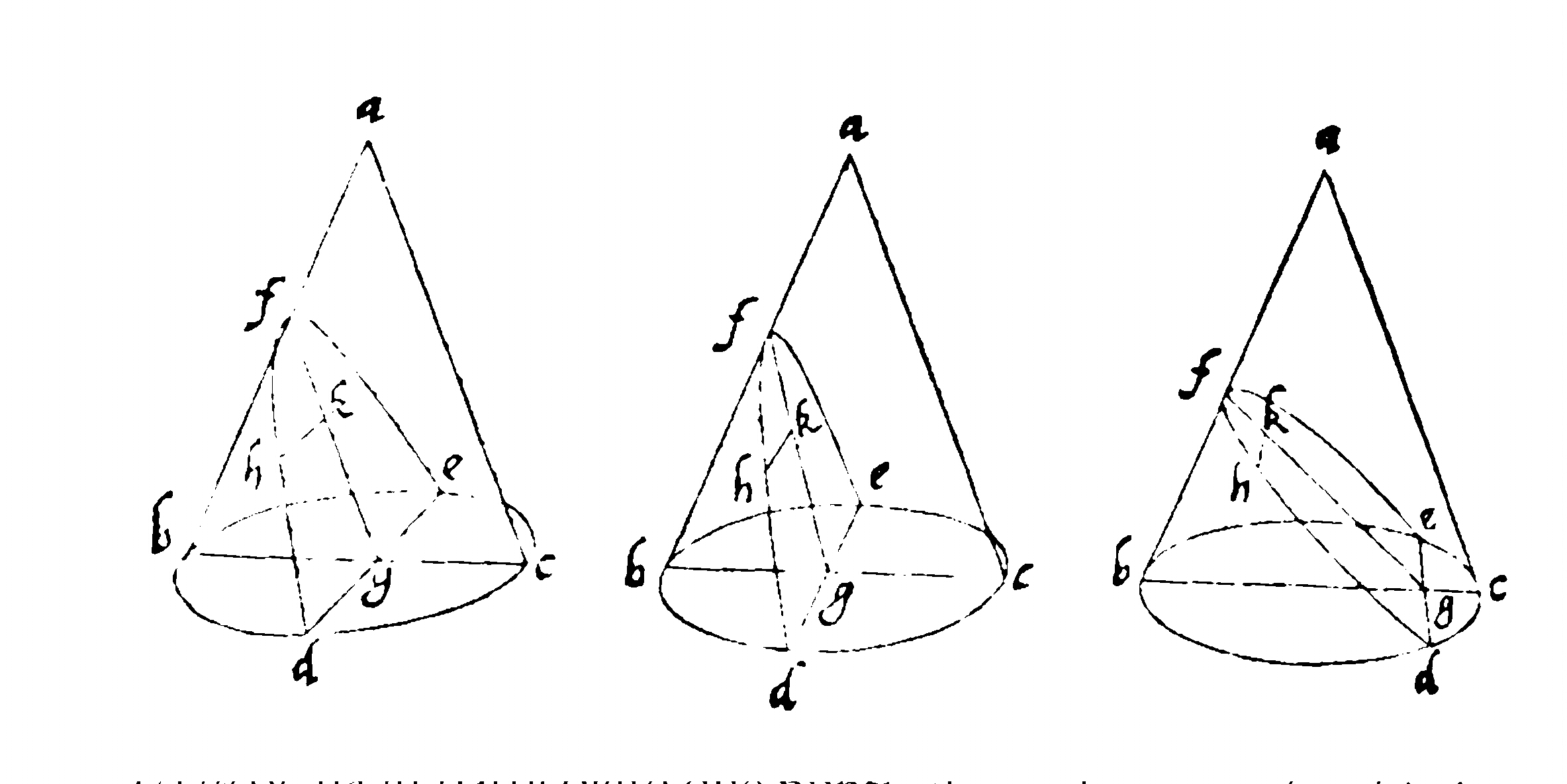
If the plane of the section then passes through the vertex of the cone
the section will be a point in case 1 and 2, a straight line in case 3
and a couple of lines in case 4. Thus, by intersecting a cone with
a plane, straight lines, circles and even three new curves, the ellipse,
the parabola and the hyperbole can be obtained.
 The most extensive antique study regarding conic sections
comes to us from Apollonius of Perga (III-II centuries B. C.).
Among other things, Apollonius demonstrates a series of properties which
lead to important applications in the fields of Science and
Technology.
The most extensive antique study regarding conic sections
comes to us from Apollonius of Perga (III-II centuries B. C.).
Among other things, Apollonius demonstrates a series of properties which
lead to important applications in the fields of Science and
Technology.
In the ellipse there are two points, called focuses, placed on the
longer diameter so that the sum of the distances
of any point of the curve from the focuses is the same. This factor
can be used to trace an ellipse which is very approximate, but
accurate enough to make, for example, elliptic flowerbeds (in fact it is
known as the gardener ellipse).
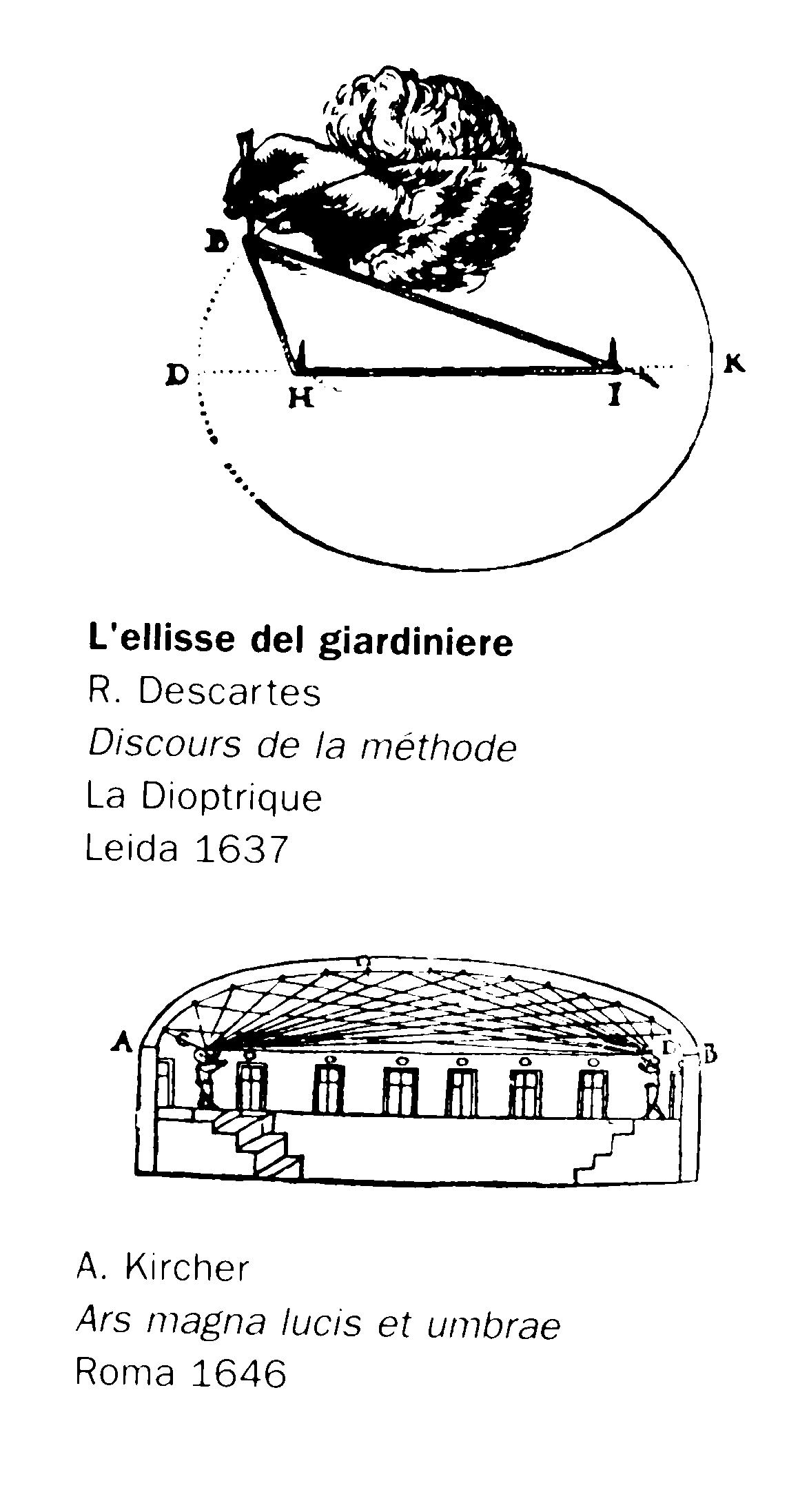
A second property of the focuses of an ellipse consists in the fact
that the perpendicular to the ellipse in any point divides the
angle formed by the segments joining this point to the two focuses in half.
Consequently, a ray of light originating from one of the focuses, and
reflected on the ellipse, passes through the other focus.
The same happens with sound waves. If one speaks standing in one of the
focuses of an elliptic vault room, the sound waves will be reflected
by the vault and will gather in the other focus.
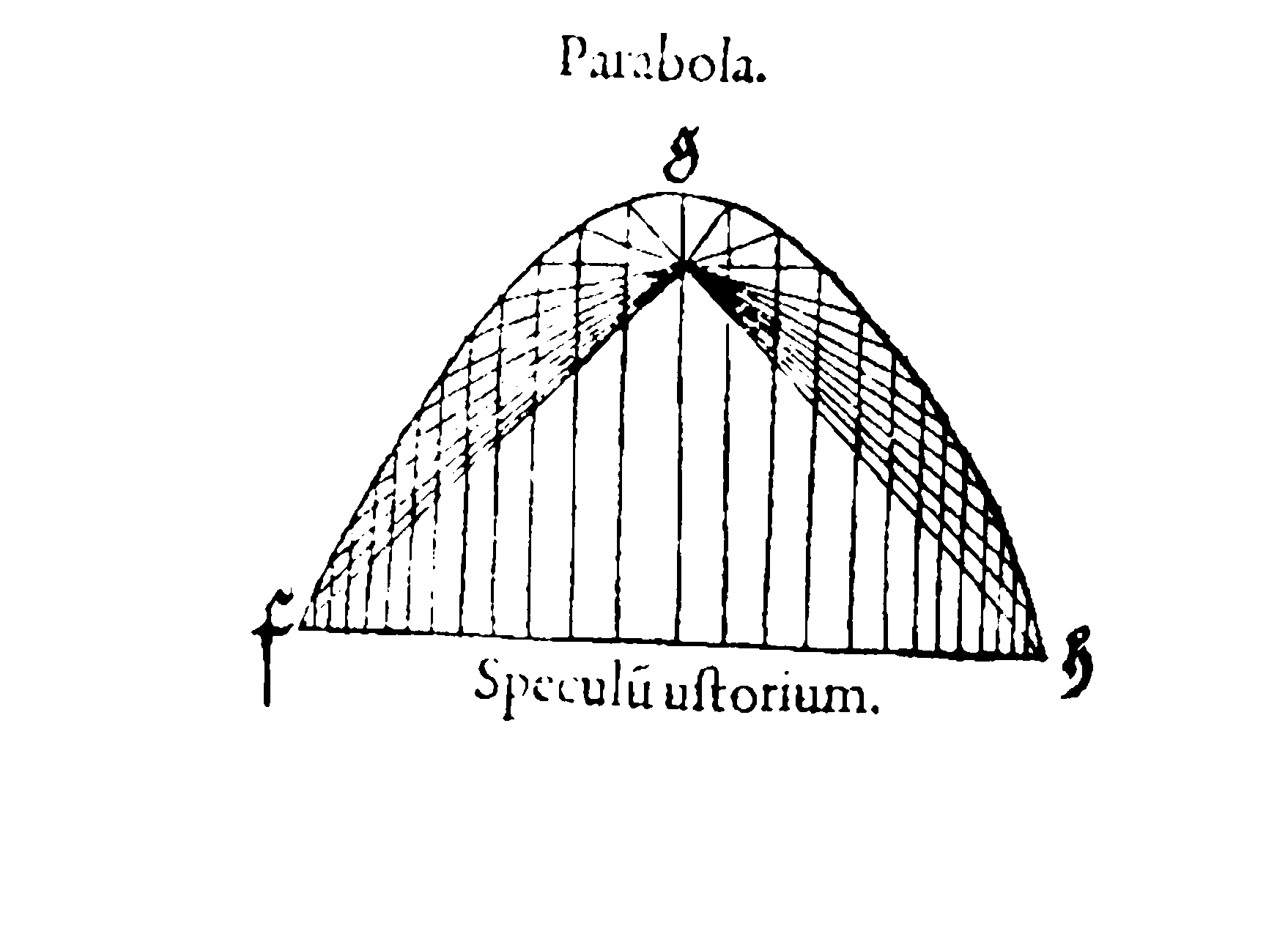
In the circle both focuses are in the centre. As the ellipse gets longer
the focuses get further apart. The parabola has only one focus, the other
one has (so to speak) gone to infinity. The rays that come from this focus
and go to infinity are parallel lines. Reflecting on the parabola
these rays will gather in the remaining focus.
Therefore, if we want to gather some parallel lines (or practically parallel,
like sun rays, for example) in a certain point, we'll need to use a glass
with the shape of a parabola. In so doing it is possible to construct
a burning glass, capable of burning a piece of paper or wood put in
its focus.
The legend - for that is how it should be considered - according to which
Archimedes (III century B.C.) burnt Roman ships with a burning mirror gave
rise to a considerable amount of reseach in this direction until
the late 17th century.
 The big radio telescopes and parabolic antennas used to receive television
transmissions from satellites, work according to the same principle.
The practically parallel signals (considering the great distance they come from),
reverberate on the antenna and are gathered in the receiver placed
in its focus, thus increasing considerably the input capacity. In other words,
the parabolic antenna works as an amplifier, or even better as a condenser
of signals, otherwise too feeble, coming from satellites.
The big radio telescopes and parabolic antennas used to receive television
transmissions from satellites, work according to the same principle.
The practically parallel signals (considering the great distance they come from),
reverberate on the antenna and are gathered in the receiver placed
in its focus, thus increasing considerably the input capacity. In other words,
the parabolic antenna works as an amplifier, or even better as a condenser
of signals, otherwise too feeble, coming from satellites.
What happens with the hyperbole is slighly more complicated. If we
stand on the outside, a ray directed to one focus is reflected in the direction
of the other focus. On the inside, a ray provening from from one focus, after
a reflection on the hyperbole will seem to provene from the other focus.